ISSUE 1: When is the intercept the mean?
When fitting ARIMA models, R calls the estimate of the mean, the estimate of the intercept. This is ok if there's no AR term, but not if there is an AR term. For example, suppose x(t) = α + φ*x(t-1) + w(t) is stationary. Then taking expectations we have μ = α + φ*μ or α = μ*(1-φ). So, the intercept, α, is not the mean, μ, unless φ=0. In general, the mean and the intercept are the same only when there is no AR term. Here's a numerical example:
# generate an AR(1) with mean 50
set.seed(66) # so you can reproduce these results
x = arima.sim(list(order=c(1,0,0), ar=.9), n=100) + 50
mean(x)
[1] 50.60668 # the sample mean is close
arima(x, order = c(1, 0, 0))
Coefficients:
ar1 intercept <-- here's the problem
0.8971 50.6304 <-- or here, one of these has to change
s.e. 0.0409 0.8365
The result is telling you the estimated model is
x(t) = 50.6304 + .8971*x(t-1) + w(t)
whereas, it should be telling you the estimated model is
x(t)−50.6304 = .8971*[x(t-1)−50.6304] + w(t)
or
x(t) = 5.21 + .8971*x(t-1) + w(t). Note that 5.21 = 50.6304*(1-.8971).
The easy thing to do is simply change "intercept" to "mean":
Coefficients:
ar1 mean
0.8971 50.6304
s.e. 0.0409 0.8365
I should mention that I reported this flub to the R folks, but I was told that it is a matter of opinion. But, if you use ar.ols, you get anotheR opinion:
ar.ols(x, order=1, demean=F, intercept=T)Note that arima() uses MLE, whereas ar.ols() uses OLS to fit the model, and hence the differences in the estimates. One thing is certain, the use of the term intercept in R is open to interpretation, which is not exactly an optimal situation.
Coefficients:
1
0.9052 <-- estimate of φ
Intercept: 4.806 (2.167) <-- yes, it IS the intercept as you know and love it
ISSUE 2: Why does arima fit different models for different orders? And what does xregdo?
When fitting ARIMA models with R, a constant term is NOT included in the model if there is any differencing. The best R will do by default is fit a mean if there is no differencing [type ?arima for details]. What's wrong with this? Well (with a time series in x), for example:
arima(x, order = c(1, 1, 0)) #(1)
will not produce the same result as
arima(diff(x), order = c(1, 0, 0)) #(2)
because in (1), R will fit the model [with ∇x(s) = x(s)-x(s-1)]
∇x(t)= φ*∇x(t-1) + w(t)
whereas in (2), R will fit the model
∇x(t) = α + φ*∇x(t-1) + w(t).
If there's drift (i.e., α is NOT zero), the two fits can be extremely different and using (1) will lead to an incorrect fit and consequently bad forecasts (see Issue 3 below).
If α is NOT zero, then what you have to do to correct (1) is use xreg as follows:
arima(x, order = c(1, 1, 0), xreg=1:length(x)) #(1+)
Why does this work? In symbols, xreg = t and consequently, R will replace x(t) with x(t)-β*t; that is, it will fit the model
∇[x(t) - β*t] = φ*∇[x(t-1) - β*(t-1)] + w(t).
Simplifying,
∇x(t) = α + φ*∇x(t-1) + w(t) where α = β*(1-φ).
If you want to see the differences, generate a random walk with drift and try to fit an ARIMA(1,1,0) model to it. Here's how:
set.seed(1) # so you can reproduce the results
v = rnorm(100,1,1) # v contains 100 iid N(1,1) variates
x = cumsum(v) # x is a random walk with drift = 1
plot.ts(x) # pretty picture...
arima(x, order = c(1, 1, 0)) #(1)
Coefficients:
ar1
0.6031
s.e. 0.0793
arima(diff(x), order = c(1, 0, 0)) #(2)
Coefficients:
ar1 intercept <-- remember, this is the mean of diff(x)
-0.0031 1.1163 and NOT the intercept
s.e. 0.1002 0.0897
arima(x, order = c(1, 1, 0), xreg=1:length(x)) #(1+)
Coefficients:
ar1 1:length(x) <-- this is the intercept of the model
-0.0031 1.1169 for diff(x)... got a headache?
s.e. 0.1002 0.0897
Let me explain what's going on here. The model generating the data is
x(t) = 1 + x(t-1) + w(t)
where w(t) is N(0,1) noise. Another way to write this is
[x(t)-x(t-1)] = 1 + 0*[x(t-1)-x(t-2)] + w(t)
or
∇x(t) = 1 + 0*∇x(t-1) + w(t)
so, if you fit an AR(1) to ∇x(t), the estimates should be, approximately, ar1 = 0 and intercept = 1.
Note that (1) gives the WRONG answer because it's forcing the regression to go through the origin. But, (2) and (1+) give the correct answers expressed in two different ways.
ISSUE 3: Why does predict.Arima give strange forecasts?
If you want to get predictions from an ARIMA(p,d,q) fit when there is differencing (i.e., d > 0), then the previous issue continues to be a problem. Here's an example using the global temperature data from Chapter 3. In what you'll see below, the first method gives the wrong results and the second method gives the correct results. I think it's just best to stay away from the first method. If you use sarima and sarima.for, then you'll avoid these problems.
u=read.table("/mydata/globtemp2.dat") # read the data
gtemp=ts(u[,2],start=1880,freq=1) # yearly temp in col 2
fit1=arima(gtemp, order=c(1,1,1))
fore1=predict(fit1, 15)
nobs=length(gtemp)
fit2=arima(gtemp, order=c(1,1,1), xreg=1:nobs)
fore2=predict(fit2, 15, newxreg=(nobs+1):(nobs+15))
par(mfrow=c(2,1))
ts.plot(gtemp,fore1$pred,col=1:2,main="WRONG")
ts.plot(gtemp,fore2$pred,col=1:2,main="RIGHT")
Here's the graphic:
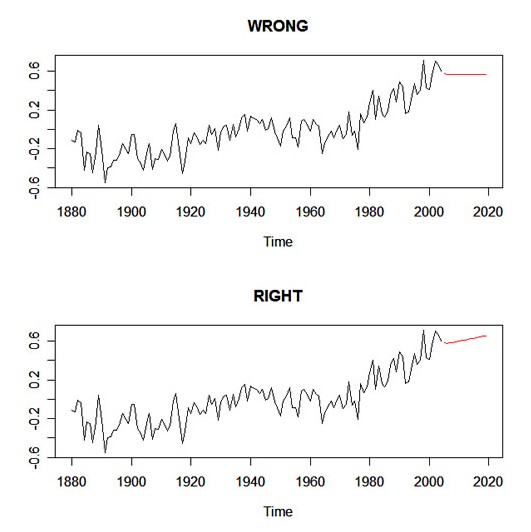 |
ISSUE 4: tsdiag.Arima gives the wrong p-values
If you use tsdiag() for diagnostics after an ARIMA fit, you will get a graphic that looks like this:
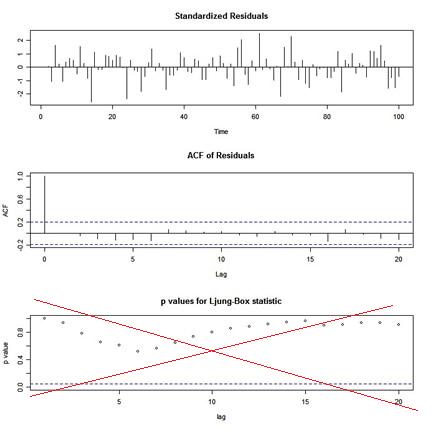 |
Comentarios
Publicar un comentario